SICP lambda icon

SICP-JS Solutions

Chapter 1 - Building Abstraction with Functions

1.2.1 Functions and the Process They Generate 1

This part includes exercise 1.9 - 1.19

Exercise 1.9

  • functions:

    // Recursive
    function plus(a, b){
      return a === 0 ? b : inc(plus(dec(a), b));
    }
    

    // Iterative
    function plus(a, b){
      return a === 0 ? b : plus(dec(a), inc(b));
    }

The evaluation process of the iterative/recursive version of plus(a, b):

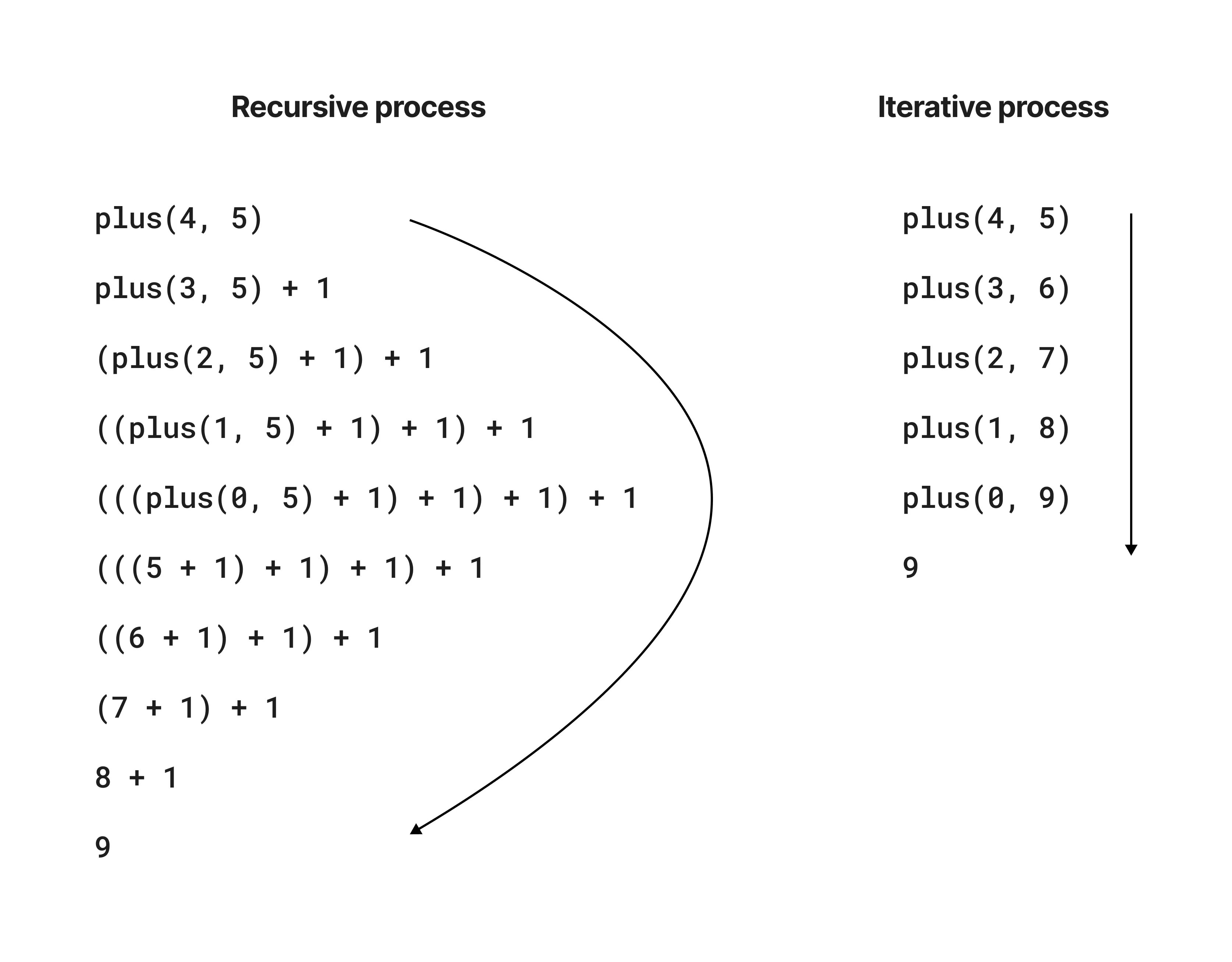
Exercise 1.9

Exercise 1.10

The evaluation of the Ackermann’s function:

Ackermann.js
function A(x, y) {
  return y === 0
         ? 0
         : x === 0
         ? 2 * y
         : y === 1
         ? 2
         : A(x - 1, A(x, y - 1));
}


console.log("\n==========Exercise 1.10==========");
console.log("The result of A(1, 10): ", A(1, 10));
console.log("The result of A(2, 4): ", A(2, 4));
console.log("The result of A(3, 3): ", A(3, 3));

output:

==========Exercise 1.10==========
The result of A(1, 10):  1024
The result of A(2, 4):  65536
The result of A(3, 3):  65536

Mathematical definitions for the provided functions:

  • function 1:

    function f(n) { return A(0, n); }

    The math expression of f(n) is: 2n2n

  • function 2:

    function g(n) { return A(1, n); }

    Function expansion:

    A(1, n)
    A(0, A(1, n - 1)) = 2 * A(1, n - 1)
    2 * A(0, A(1, n - 2)) = 2 * 2 * A(1, n - 2)
    ...
    2 * 2 * 2 * 2 * ... * A(1, 0) = 2 * 2 * 2 * 2 * ... * 2

    Therefore, the math expression of g(n) is: 2n2^n

  • function 3:

    function h(n) { return A(2, n); }

    Function expansion:

    A(2, n)
    A(1, A(2, n - 1)) = 2 ** (A(2, n - 1))
    2 ** 2 * (A(1, n - 2)) = 2 ** (2 ** A(2, n - 2))
    ...
    2 ** (2 ** (2 ** (2 ** (...** (2 * 0)...))))

    Therefore, the math expression of h(n) is: (n−1)2=222⋅⋅2^{(n-1)}2 = 2 ^{2^{2^{\cdot ^{\cdot ^{2}}}}}

  • function 4:

    function k(n) { return 5 * n * n; }

    The math expression of k(n) is: 5n25n^2

Exercise 1.11

The JavaScript version of the math function ff in both recursive and iterative methods

exercise_1_11.js
//recursive method
function fr(n) {
  return n < 3
         ? n
         : fr(n - 1) + 2 * fr(n - 2) + 3 * fr(n - 3);
}


//iterative method
function fi(n) {
  return fi_iter(2, 1, 0, n);
}
function fi_iter(a, b, c, n) {
  return n === 0
         ? c
         : n === 1
          ? b
          : fi_iter(a + 2 * b + 3 * c, a, b, n - 1);
}


console.log("\n==========Exercise 1.11==========");
console.time("f(n) recursive method total time: ");
console.log("result of f(20) recursive method: ", fr(20));
console.timeEnd("f(n) recursive method total time: ");
console.time("f(n) iterative method total time: ");
console.log("result of f(20) iterative method: ", fr(20));
console.timeEnd("f(n) iterative method total time: ");

output:

==========Exercise 1.11==========
result of f(20) recursive method:  10771211
f(n) recursive method total time: : 1.574ms
result of f(20) iterative method:  10771211
f(n) iterative method total time: : 0.529ms

Exercise 1.12

Pascal’s triangle:

exercise_1_12.js
function pascalTriangle(row, col) {
  return col === 0 || col === row
    ? 1
    : pascalTriangle(row - 1, col - 1) + pascalTriangle(row - 1, col);
}


// Helper function to print out the pascal triagnle
function printPascalTriangle(n) {
  const totalPad = n - 1;
  for (let row = 0; row < n; row++) {
    let str = "".padStart(totalPad - row, " ");
    for (let col = 0; col < row + 1; col++) {
      str += pascalTriangle(row, col);
      str += " ";
    }
    console.log(str);
  }
}


console.log("\n==========Exercise 1.12==========");
console.log("A pasccal triangle with 5 rows:");
printPascalTriangle(5);

output:

==========Exercise 1.12==========
A pasccal triangle with 5 rows:
    1
   1 1
  1 2 1
 1 3 3 1
1 4 6 4 1

Exercise 1.13

Step 1

We assume that Fib(n)=rnFib(n) = r^n, and the recursive format of Fib(n)Fib(n) can be expressed as:
rn=rn−1+rn−2r^n = r^{n - 1} + r ^ {n - 2} Assuming that r≠0r \neq 0, we divide both sides by rn−2r^{n - 2}, and get: r2=r+1r^2 = r + 1 Given that in the quadratic formula ax2+bx+c=0ax^2 + bx + c = 0:

x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

We can solving the equation:

r=1±52r = \frac{1 \pm \sqrt{5}}{2}

Then we can denote each solution as:

ϕ=1+52,ψ=1−52\phi = \frac{1 + \sqrt{5}}{2}, \quad \psi = \frac{1 - \sqrt{5}}{2}

Step 2

The Fibonacci sequence if a linear homogeneous recurrence relation of the second degree, its general solution is a linear combination of the solutions found:

Fib(n)=A(ϕn)+B(ψn)Fib(n) = A(\phi^n) + B(\psi^n)

For n=0,Fib(0)=0n = 0, Fib(0) = 0 and n=1,Fib(1)=1n = 1, Fib(1) = 1, we can find the values of AA and BB:

A+B=0Aϕ+Bψ=1A=15,B=−15A + B = 0 \\ A\phi + B\psi = 1 \\ A = \frac{1}{\sqrt{5}}, \quad B = -\frac{1}{\sqrt{5}} \\

Step 3

Now we subsitute AA and BB back into the general solution:

Fib(n)=15ϕn−15ψn=ϕn−ψn5Fib(n) = \frac{1}{\sqrt{5}}\phi^n - \frac{1}{\sqrt{5}}\psi^n = \frac{\phi^n - \psi^n}{\sqrt{5}}

With n increasing, ψn\psi^n will gradually approaching 0, therefore Fib(n)Fib(n) is the closest integer to ϕn/5\phi^n / \sqrt{5}

Exercise 1.14

The tree-recursive process generated in computing count_change(11) function:

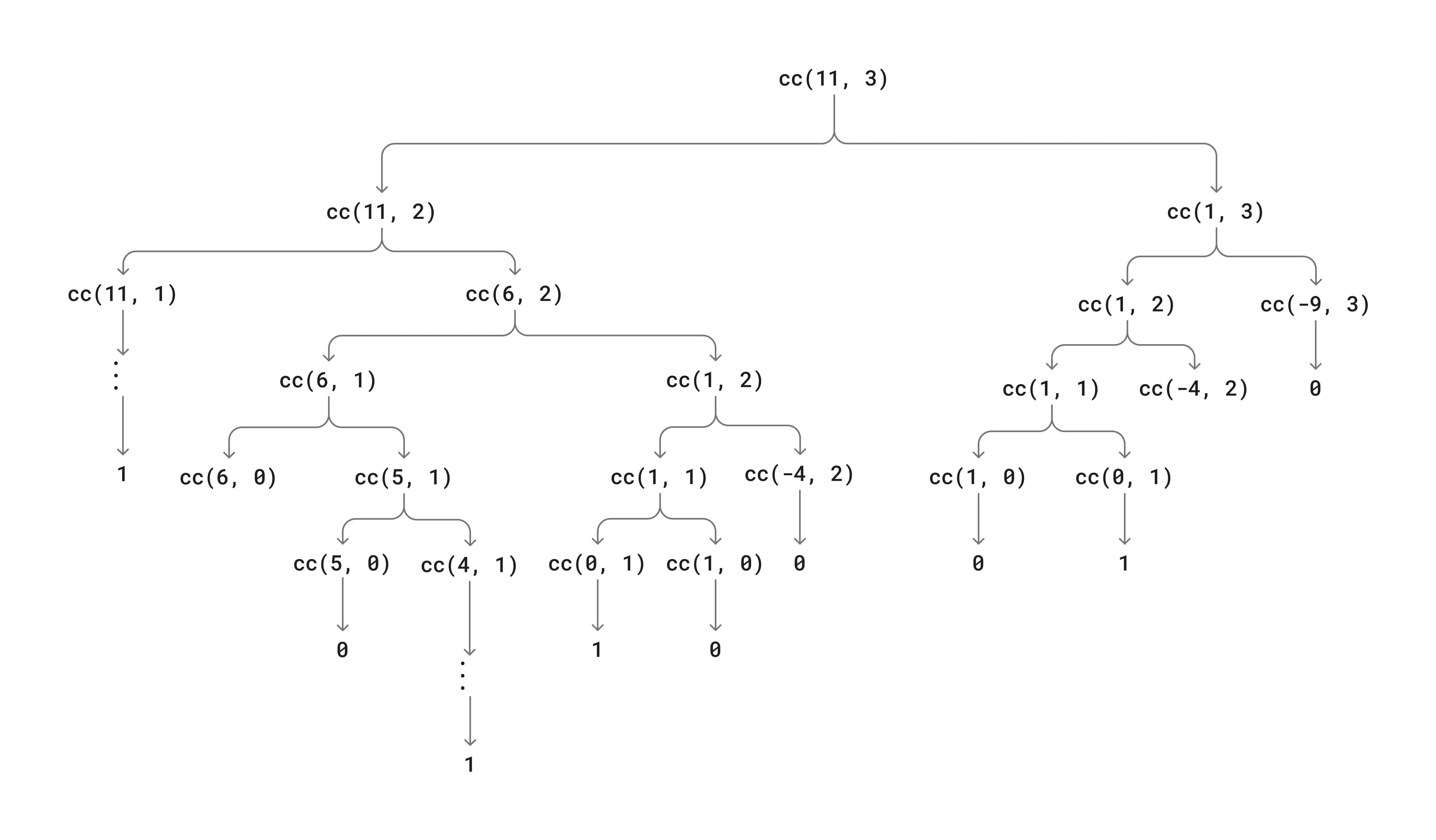
Exercise 1.14

The step has Θ(2N)\Theta(2^N) order of growth, where NN is the target amount; The order of growth of the space is Θ(N⋅m)\Theta(N \cdot m), where NN is the target amount and mm is the number of coin dominations, because each combination of amount and coin denomication is calculated only once.

Exercise 1.15

Compute the sine value of an angle:

exercise_1_15.js
let runCounts = 0;


function cube(x) {
  return x * x * x;
}


function p(x) {
  runCounts += 1;
  return 3 * x - 4 * cube(x);
}


function sine(angle) {
  return !(Math.abs(angle) > 0.1) ? angle : p(sine(angle / 3));
}


console.log("\n==========Exercise 1.15==========");
console.log(sine(3.14));
console.log(
  "The total time of the function p runs when evaluation sine(3.14) is: ",
  runCounts
);

output:

==========Exercise 1.15==========
0.0008056774674223277
The total time of the function p runs when evaluation sine(3.14) is:  4

The number of steps of sine(angle) is Θ(log⁡3Nm)\Theta(\log_3\frac{N}{m}), where NN is the angle, and mm is the precision;
The space complexity is also Θ(log⁡3Nm)\Theta(\log_3\frac{N}{m}), reflecting the depth of the recursive calls.

Exercise 1.16

The iterative version of the fast-exponentiation algorithm:

exercise_1_16.js
function fastExptIter(b, n) {
  if (n === 0) return 1;
  a = 1;
  while (n > 0) {
    if (n % 2 === 1) {
      a *= b;
      n -= 1;
    } else {
      b *= b;
      n /= 2;
    }
  }
  return a;
}


console.log("\n==========Exercise 1.16==========");
console.log(
  "Our result of 2^5: ", fastExptIter(2, 5),
  "; Correct answer", 2 ** 5
);


console.log(
  "Our result of 3^8:", fastExptIter(3, 8),
  "; Correct answer", 3 ** 8
);


console.log(
  "Our result of 4^11:", fastExptIter(4, 11),
  "; Correct answer", 4 ** 11
);

output:

==========Exercise 1.16==========
Our result of 2^5: 32 ; Correct answer 32
Our result of 3^8: 6561 ; Correct answer 6561
Our result of 4^11: 4194304 ; Correct answer 4194304

Exercise 1.17

A faster version of times(a, b) function with Θ(log⁡n)\Theta(\log n) complexity:

exercise_1_17.js
function double(a) {
  return a * 2;
}


function halve(b) {
  return b / 2;
}


function fastTimes(a, b) {
  return b === 0
    ? 0
    : b % 2 == 1
      ? a + fastTimes(a, b - 1)
      : fastTimes(double(a), halve(b));
}


console.log("\n==========Exercise 1.17==========");
console.log(
  "Our result of 5 * 9:", fastTimes(5, 9),
  "; Correct answer: ", 5 * 9
);
console.log(
  "Our result of 423 * 12:", fastTimes(423, 12),
  "; Correct answer: ", 423 * 12
);

output:

==========Exercise 1.17==========
Our result of 5 * 9: 45 ; Correct answer:  45
Our result of 423 * 12: 5076 ; Correct answer:  5076

Exercise 1.18

The iterative version of the fastTimes(a, b):

exercise_1_18.js
function fastTimesIter(a, b) {
  let ans = 0;
  while (b > 0) {
    if (b % 2 === 1) {
      ans += a;
      b -= 1;
    } else {
      a = double(a);
      b = halve(b);
    }
  }
  return ans;
}


console.log("\n==========Exercise 1.18==========");
console.log(
  "Our result of 5 * 9:", fastTimesIter(5, 9),
  "; Correct answer: ", 5 * 9
);
console.log(
  "Our result of 423 * 12:", fastTimesIter(423, 12),
  "; Correct answer: ", 423 * 12
);

output:

==========Exercise 1.18==========
Our result of 5 * 9:  45 ; Correct answer:  45
Our result of 423 * 12:  5076 ; Correct answer:  5076

Exercise 1.19

Applying the transformation matrix in computing fibonacci numbers to achieve Θ(log⁡n)\Theta(\log n) complexity. This exercise is a bit tricky, please refer to Kaldewaji 1990, page 88 for the details of the expressions of the transformation matrix:

exercise_1_19.js
// 1.19
function fib(n) {
  return fibIter(1, 0, 0, 1, n);
}


function fibIter(a, b, p, q, count) {
  return count === 0
    ? b
    : count % 2 === 0
      ? fibIter(a, b, p * p + q * q, p * q + p * q + q * q, count / 2)
      : fibIter(b * q + a * q + a * p, b * p + a * q, p, q, count - 1);
}


console.log("\n==========Exercise 1.19==========");
console.log("Result of faster fib(3): ", fib(3));
console.log("Result of faster fib(10): ", fib(10));
console.log("Result of faster fib(20): ", fib(20));

output:

==========Exercise 1.19==========
Result of faster fib(3):  2
Result of faster fib(10):  55
Result of faster fib(20):  6765